Одним из наиболее точных методов измерения сопротивлений является мостовой метод, при котором неизвестное измеряемое сопротивление сравнивают с тремя известными. На рис. I показана схема моста постоянного тока. Четыре сопротивления: R1, R2, R3 и RХ соединены в замкнутый четырехугольник, стороны которого образуют плечи моста. В одну из диагоналей моста включают источник тока, в другую – магнитоэлектрический индикатор высокой чувствительности. Если в цепи прибора тока нет, мост считается уравновешенным. Это может быть только при равенстве потенциалов
в точках C и D т.е. jC -jD =0. 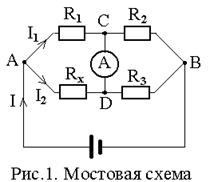
Уравновешивают мост, подбирая сопротивления R2 или R3. В уравновешенном мосте произведения сопротивлений противоположных плеч равны: R1×R3 =R2 ×RХ .
Докажем это соотношение, пользуясь вторым правилом Кирхгофа. Для замкнутых контуров ACDA и CBDC можно записать следующие уравнения (при условии равновесия моста):
Решая эту систему уравнений, получим:
Из этого соотношения видно, что равновесие моста может быть получено двумя способами: при постоянном отношении постоянных сопротивлений R3/R2 изменением сопротивления R1, или при постоянном сопротивлении одного плеча R1 изменением соотношения сопротивлений двух других плеч R3/R2 .
В зависимости от способа получения равновесия моста существуют различные его конструкции. На рис. 2 показана мостовая схема, в которой
равновесие моста достигается вторым способом. Эта схема называется мостом Уитстона.
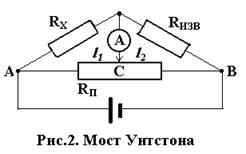
Так как сопротивления плеч потенциометра RП: RАC и RCB пропорциональных их длинам l1 и l2, тогда
Таким образом, процесс измерения сопротивления с помощью моста Уитстона сводится к балансировке моста и измерению длин плеч l1 и l2 потенциометра RП. Последнее может осуществляться с помощью линейки или шкалы, смонтированной на потенциометре.
Точность измерения сопротивлений определяется точностью уравновешенности моста, которая существенно зависит от чувствительности индикатора и величины напряжения питания.
Мостовые схемы образуют обширный класс измерительных цепей, широко используемый в радиотехнике, автоматике и других областях техники.
Описание установки, измерения и обработка результатов измерений
Электрическая схема передней панели лабораторной установки приведена на рис.3.
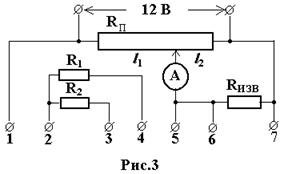
ВНИМАНИЕ! В установке для данной лабораторной работы используется высокоточный круговой потенциометр, который размещен горизонтально на передней панели установки. Его шкала расположена впереди, а ручка вращения сзади. Максимальный угол поворота ручки потенциометра 330 0 . Шкала потенциометра разбита на 33 части (по 10 0 ) Внимательно изучите шкалу потенциометра.
Работу выполняют в следующем порядке:
1. С помощью проводов собирают на лабораторном стенде схему моста Уитстона, включив в нее резистор с неизвестным сопротивлением R1. Для этого необходимо соединить клеммы I и 2, а также 4 и 5.
2. Подключают источник питания 12 В и балансируют мост, перемещая движок потенциометра до тех пор, пока стрелка индикатора (миллиамперметра А) не установится на отметке "О".
3. Измеряют длины плеч потенциометра и результат заносят в таблицу 1.
ВНИМАНИЕ! При использовании кругового потенциометра длины плеч l1 и l2 необходимо представить в угловой мере, как: j1 и j2 . В этом случае формулы (1),(2) будут иметь вид:
Измерения повторяют не менее 3 раз. При каждом последующем измерении (для снятия второго и следующих отсчетов ) необходимо повернуть ручку переменного резистора (расположен в левом верхнем углу на передней панели лабораторной установки) на угол »10-20 0 , а затем выполнить балансировку моста.
4. В той же последовательности измеряют сопротивление резистора R2 , а затем сопротивление последовательно и параллельно соединенных резисторов R1 и R2
5. Результаты всех измерений и вычислений заносят в таблицу I.
| RИЗВ Ом | j1 град | j2 град | Rx Ом | 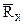 Ом Ом |
D Rx Ом | 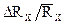 |
| Резистор R1 | ||||||
| Резистор R2 | ||||||
| Последовательное соединение R1 и R2 | ||||||
| Параллельное соединение R1 и R2 |
6. Погрешность измерений вычисляют по формуле:
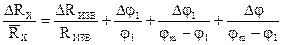 (4)
(4)
В формуле (4): ∆RИЗВ/RИЗВ принять равным 5% , Dj=2,5 0 (половина наименьшего деления шкалы кругового потенциометра).
Формулу (4) можно упростить, полагая j1=jm/2 (в этом случае точность измерений наибольшая) и Dj1=Dj. Сделайте это самостоятельно.
7. Результаты измерений сопротивлений при их последовательном и параллельном соединениях сравнивают с величинами, рассчитанными по известным формулам: RПОСЛ=R1+R2 и RПАРАЛ =(R1× R2) /(R1+R2).
Вывод записать письменно.
ИЗУЧЕНИЕ ЗАКОНОВ ОМА ДЛЯ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Обобщённый закон Ома.
Рассмотрим участок электрической цепи, изображенный на рис.1.

Подчеркнём, что нами выбран участок из некоторой произвольной электрической цепи. В ней могут быть другие ЭДС, не входящие в выделенный участок, под действием которых ток по данному участку может течь и навстречу данной ЭДС Е.
Примечание. 1) На рис.1 вертикальными линиями показано изображение источника тока, имеющего характеристики: ЭДС E и внутреннее сопротивление r. Часто вместо слов источник тока говорят: ЭДС. 2)Терминология: участок цепи, содержащий ЭДС и сопротивление R называется неоднородным, а содержащий только сопротивление R –однородным.
Найдем взаимосвязь между величинами I, Е, j1, j2, j3 для рассматриваемого участка. Обозначим общее сопротивление между точками 1-3 через R: R=R+r, гдеR-сопротивление внешнего участка цепи, r- внутреннее сопротивление источника ЭДС.
Выразим потенциал точки I через потенциал точки 3.
Дата добавления: 2015-10-06 ; просмотров: 3795 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Измерительный мост, позволяющий определять величину неизвестного электрического сопротивления, был изобретён британским учёным Самуэлом Кристи в 1833 году, и позже модернизирован и популяризирован другим британским учёным, Чарьзом Витстоном в 1843 году.
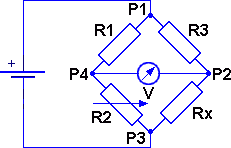
Схема измерительного моста Уинстона.
P1 – P3 – диагональ питания; P2 – P4 – измерительная диагональ моста;
R1, R2 – левое плечо, R3, Rx – правое плечо моста.
Принцип работы
Принцип измерения неизвестного сопротивления основан на уравнивании отношений сопротивлений в обоих плечах моста, при этом гальванометр, включённый между этими плечами, будет показывать нулевое напряжение. На рисунке Rx – это неизвестное сопротивление, которое требуется измерить. R1, R2 и R3 – резисторы с известными значениями сопротивлений, причём резистор R2 переменный. Если отношение двух известных сопротивлений в плече R2/R1 равно отношению сопротивлений в плече Rx/R3, то в этом случае напряжение между точками схемы P2 и P4 будет равно нулю, и через гальванометр V ток не будет течь. Если же мост разбалансирован, то отклонение гальванометра будут указывать на то, что сопротивление резистора R2 слишком большое или слишком маленькое. Переменный резистор R2 регулируют до тех пор, пока гальванометр не укажет на ноль.
По гальванометру можно определять отсутствие тока в цепи с очень большой точностью. Следовательно, если резисторы R1, R2 и R3 – высокоточные, то неизвестное сопротивление Rx может быть измерено с большой точностью. Небольшие изменения сопротивления Rx разбалансируют измерительный мост, что обнаруживается по показанию гальванометра.
При сбалансированном мосте выполняется равенство R2/R1 = Rx/R3.
Отсюда Rx = R3*R2 / R1
В случае если сопротивления R1, R2 и R3 известны, а резистор R2 – постоянный, то неизвестное сопротивление Rx может быть рассчитано с помощью законов Кирхгофа. Этот метод измерения часто используется при применении измерительного моста в тензометрии, совместно с тензодатчиком, так как считать показания с гальванометра получится гораздо быстрее, чем балансировать мост переменным резистором.
Расчёт
Используя первый закон Кирхгофа, найдём токи, протекающие в узлах P2 и P4:
Далее с помощью второго закона Кирхгофа найдём напряжения в контурах P1-P2-P4 и P2-P3-P4:
Мост сбалансирован, следовательно IG = 0, так что вторая система уравнений сократится:
Решая эту систему уравнений, получим:
Из первого закона Кирхгофа следует, что I3 = Ix и I1 = I2. Следовательно величина неизвестного сопротивления Rx будет определятся по формуле:
Если известны сопротивления всех четырёх резисторов и величина питающего напряжения Uпит, а сопротивление гальванометра достаточно высокое, так что током IG, протекающим через него можно пренебречь, то напряжение U между точками моста P2 и P4 может быть найдено путём расчёта каждого из делителей напряжения, вычтя затем напряжение на одном делителе из напряжения на другом делителе. В этом случае получится следующее уравнение:
Напряжение питания Uпит можно вынести за скобки, в этом случае получится выражение:
Где U – напряжение в точке P2 относительно точки P4.
Измерительный мост Уинстона иллюстрирует концепцию дифференциальных измерений, результаты которых могут быть очень точными. Различные разновидности моста Уинстона используются для измерения ёмкости, индуктивности, импеданса и других величин. Одной из разновидностей моста является мост Кельвина, специально предназначенный для измерения малых сопротивлений. Во многих случаях измерение величины неизвестного сопротивления связано с измерением некоторых физических параметров, таких как сила, температура, давление и т.д., здесь в качестве измеряемого сопротивления используется соответствующий резистивный датчик.
В 1865 году Джеймс Максвелл применил измерительный мост Уинстона, питаемый переменным током, для измерения индуктивности, и в 1926 году Алан Блюмлейн подверг этот мост усовершенствованию.
Модификации основной схемы измерительного моста
Мост Уинстона является основной схемой измерительных мостов, но так же существуют различные его модификации, с помощью которых можно проводить измерения различных типов сопротивлений, когда основная схема моста для этого не подходит. Вот несколько разновидностей основной схемы измерительного моста:
 Мостовая схема — схема соединения элементов электрической цепи (сопротивлений, выпрямительных диодов и т.д.), характеризующаяся наличием мостовой ветви между двумя точками схемы, не соединенными непосредственно с источником электрической энергии. В основу мостовой схемы положена схема моста Уитстона (рис. 1).
Мостовая схема — схема соединения элементов электрической цепи (сопротивлений, выпрямительных диодов и т.д.), характеризующаяся наличием мостовой ветви между двумя точками схемы, не соединенными непосредственно с источником электрической энергии. В основу мостовой схемы положена схема моста Уитстона (рис. 1).
Принцип действия мостовой схемы основан на том, что при равенстве отношений полных сопротивлений в плечах моста Za/Zb = Z х/ Zd в диагонали моста (в индикаторном устройстве) нет тока. Повышая чувствительность нуль-индикатора, можно добиться в мостовой схеме весьма точного соблюдения равенства отношений полных сопротивлений. На этом принципе основаны мостовые измерения.
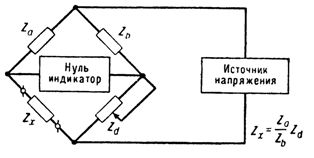
Рис. 1. Мостовая схема (схема моста Уитстона)
Источниками питания мостовых схем могут служить источники напряжения как постоянного так и переменного тока. Балансировка мостовой схемы совершенно не зависит от колебаний напряжения источника питания.
Мостовые измерения — методы измерения параметров электрических цепей на постоянном токе (сопротивления пост, току) и на переменном токе (активного сопротивления, емкости, индуктивности, взаимной индуктивности, частоты, угла потерь, добротности и др.) посредством мостовых схем. Мостовые измерения широко распространены также для электрических измерений неэлектрических величин при помощи датчиков — промежуточных преобразователей измеряемой величины в функционально связанный с ней параметр электрической цепи.
Мостовые измерения осуществляются с помощью измерит, мостов (мостовых установок), относящихся к категории приборов сравнения. В общем случае они основаны на применении некоторой электрической цепи, состоящей из нескольких известных и одного неизвестного (измеряемого) сопротивлений, питаемой одним источником и снабженной указывающим прибором.
Изменением известных сопротивлений эта цепь регулируется до достижения определенного, отмечаемого указателем, распределения напряжений на отдельных участках цепи. Очевидно, что заданному соотношению напряжений соответствует также определенное соотношение сопротивлений цепи, по которому можно вычислить неизвестное сопротивление, если остальные сопротивления известны.
Исторически первый, простейший и наиболее распространенный вариант мостовых измерений был реализован посредством четырехплечего уравновешенного моста , представляющего собой кольцевую цепь из 4 сопротивлений ("плечи" моста), в которой источник питания и указатель включаются диагонально, к противолежащим вершинам, в виде "мостов" (рис. 2).
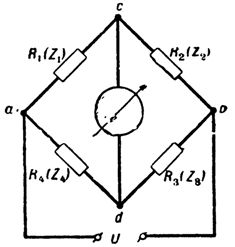
При соблюдении условия R1R3 = R2R4 (соответственно Z1Z3 = Z2Z4 на переменном токе) напряжение на выходе мостовой цепи (независимо от питающего напряжения) равно нулю (Ucd=0), т. е. мост "уравновешен", что отмечается нулевым указателем.
Состояние равновесия моста постоянного тока, соответствующее условию R1R3 = R2R4, может быть достигнуто регулировкой только одного переменного параметра и позволяет определить также только одно неизвестное сопротивление.
Для достижения комплексного условия равновесия на переменном токе Z1Z3 = Z2Z4, распадающегося при подстановке комплексных значений сопротивлений Z=R+jx на два самостоятельных условия, требуется регулировка не менее двух переменных параметров. При этом можно одновременно определять две составляющие комплексного сопротивления (например, L и R или L и Q, С и tg φ и т. д.).
Разновидностью четырехплечих мостов переменного тока являются мосты резонансные . Помимо четырехплечих применяются более сложные мостовые цепи — двойные мосты на постоянном токе (рис. 3) и многоплечие (шести- или семиплечие) — на переменном (например, рис. 4). Условия равновесия для этих цепей, естественно, отличаются от приведенных выше.
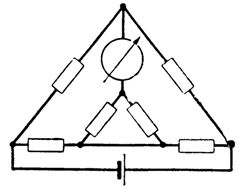
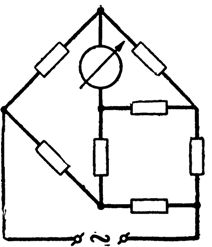
Мосты могут использоваться как в уравновешенном, так и в неуравновешенном режиме. В последнем результат измерения определяется без регулировки сопротивлений, непосредственно по току или напряжению на выходе мостовой цепи, которые являются функциями измеряемого сопротивления и напряжения источника питания (последнее должно быть стабильным). Выходной прибор при этом градуируется непосредственно в значениях измеряемой величины.

Мостовые измерения на переменном токе могут применяться еще в двух режимах: квазиуравновешенном и полууравновешенном. Последний характеризуется тем, что обычная четырехплечая цепь (рис. 2) регулируется при помощи только одного переменного параметра до получения минимального выходного напряжения (полное равновесие, т. е. Ucd =0, при котором требуется регулировка двух параметров, в данном случае недостижимо).
Момент достижения минимума напряжения Uс d может быть определен непосредственно обычным указателем на выходе цепи или более точно — косвенно — на основании, например, фазовых соотношений векторов напряжений мостовой цепи, имеющих место в момент полуравновесия.
Во втором случае эксперимент и указывающая аппаратура аналогичны применяемым при квазиуравновешенном режиме. Составляющие измеряемого сопротивления определяются: одна — по значению переменного параметра в момент полуравновесия, другая — по напряжению на выходе моста. Напряжение питания необходимо стабилизировать.

Уравновешивание измерительных мостов может производиться как непосредственно человеком (мосты с ручной наводкой), так и при помощи автоматического устройства (автоматические измерительные мосты).
Мостовые измерения применяются как для измерения значений сопротивлений, так и для определения отклонений этих значений от заданного номинала. Они относятся к числу самых распространенных и совершенных методов измерения. Серийно выпускаемые мосты имеют классы точности от 0,02 до 5 на пост, токе и от 0,1 до 5 — на переменном.

